Generative Learning Algorithms & Naive Bayes

Generative Learning Algorithms

Nếu như logistic regression là thuật toán đi tìm xác xuất p(y|x; θ) (tìm theta sao cho xác xuất của p theo x lớn nhất). thì trong bài viết này, chúng ta sẽ đi tìm hiểu một thuật toán khác, được cho là tốt hơn logistic regression về mặt hiệu năng khi dữ liệu ở dạng phân phối chuẩn.

Một ví dụ để dễ hình dung hơn, cho rằng chúng ta cần xây dựng 1 model học cách phân biệt giữa voi(y=1) và chó(y=0), dựa trên một số đặc trưng dủa động vật. Với tập dữ liệu đã cho, logistic regression hoặc perception algorithm sẽ cố gắng tìm kiếm 1 đường thẳng, quyết định ranh giới phân biệt giữa hai loài động vật trên trong tập dữ liệu. Khi cần phân loại 1 con vật mới, nó sẽ kiểm tra xem bên nào là nơi nó thuộc về dựa vào ranh giới đã thiết lập ở trên.

Có 1 giải pháp khác, thú vị không kém, đầu tiên, nhìn vào đàn voi (tập dữ liệu là các con voi), chúng ta xây dựng một model các con voi, với đàn chó, chúng ta cũng xây dựng 1 model nhìn giống như 1 đàn chó, cuối cùng, khi cần phân biệt 1 con vật mới thuộc hai nhóm trên, chúng ta sẽ kiểm tra xem nó có thuộc voi model, và kiểm tra nó có thuộc chó model (^^).

Thuật toán mà cố gắng học trực tiếp p(y|x) như logistic regression, hoặc thuật toán cố gắng ánh xạ không gian đầu vào X ra thành tập nhãn dán {0,1} như perceptron, được chung là Discriminative Algorithm. Ở đây, chúng ta nói về thuật toán thay vì tìm xác xuất của p(y|x) ta sẽ tìm xác xuất của p(x|y), model còn được gọi là generative learning, một ví dụ ở đây: nếu y chỉ ra một con vật là chó(0) hay voi(1), thì p(x|y=0) là model chỉ ra đó là những con chó trong phân phối, còn p(x|y=1) là phân phối mà các con voi đều tập trung ở đấy.

Sau đó, chúng ta sử dụng quy tắc Bayes để tìm ra model:

Với mẫu số p(x) = p(x|y = 1)p(y = 1) + p(x|y =0)p(y = 0) (dễ dàng chứng minh), do đó, chúng ta cần học p(x|y) và p(y), nếu chúng ta chỉ cần tính p(y|x) thì thực sự chúng ta không cần tính mẫu số:

Sau đây, sẽ giới thiệu hai dạng thường được dùng trong các bài toán Generative Learning Algorithm, đầu tiên là GDA.

Gaussian discriminant analysis - GDA

The multivariate normal distribution - Phân phối chuẩn đa biến

Thay vì phân phối chuẩn thường thấy với trung bình và phương sai là các số xác định, thì ở đây, chúng ta có: mean vector µ ∈ R và covariance matrix Σ ∈ R n×n, gọi là N (µ, Σ), với hàm mật độ xác suất:

Như vậy, áp dụng kiến thức về xác xuất, cho biến ngẫu nhiên X và phân phối như trên, trung bình (mean) sẽ được cho bởi:

Hiệp phương sai sẽ được tính bởi Cov(Z) = E[(Z − E[Z])(Z − E[Z])^T], nếu X tuân theo chuẩn X ∼ N (µ, Σ) thì:

Khi thay đổi phương sai, ví dụ thay đổi đường chéo ma trận (lưu ý, ma trận ở đây luôn luôn đối xứng), ta sẽ được các phân phối khác nhau:

Khi thay đổi kỳ vọng, thì sẽ di chuyển "phân phối đó":

Như vậy, quá trình học ở đây là tìm bộ tham số cho kỳ vọng và phương sai thỏa mãn với tập dữ liệu đã cho.

1.2 The Gaussian Discriminant Analysis model

Chúng ta sẽ giả sử model tuân theo các chuẩn sau, vì sao lại thế, vì thế giới này là thế !

Như thế, chúng ta có mật độ xác xuất cho từng phần cụ thể như sau:

Log-likelihood sẽ như thế này (log-likelihood là tìm giá trị bộ tham số sao cho xác suất để nó xảy ra là cao nhất).

Bằng cách tối đa hóa l, với một chút tính toán chúng ta có thể tìm được bộ tham số như sau:

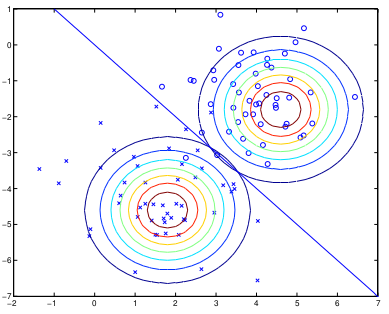
Có thể thấy, chỉ đơn giản là tính toán đơn thuần, không phải đạo hàm gì cả, chúng ta cũng có thể học từ dữ liệu, thuật toán sẽ phân loại nhìn giông snhư dưới đây:

Nhìn vào hình vẽ trên, chúng ta có thể thấy 2 contour(mặt cắt) của 2 phân phối đại diện cho 2 lớp cần phân loại, đường thẳng ở giữa là xác xuất p(y = 1|x) = 0.5.

Discussion: GDA and logistic regression

Có thể bạn chưa biết, GDA model có một mối quan hệ rất thú vị với logistic regression, nếu chúng ta xem p(y = 1|x; φ, µ 0 , µ 1 , Σ) như một hàm của x, chúng ta có thể tìm các giá trị thỏa mãn công thức dưới đây:

Một câu hỏi được đặt ra, mô hình nào tốt hơn mô hình nào ? GDA hay logistic ??

Nói chung, nếu bạn muốn hiểu, hãy comment, mình sẽ cố giải thích (tại mình cũng lười tìm hiểu), chỉ là, nếu bạn để ý, có vẻ GDA tốt hơn vì nó cố gắng fit với mỗi mô hình, nhưng điểm yếu của nó là có khi dữ liệu của mình không hoàn toàn thuộc về phân phối Gauss. Nói tóm lại, khi tập dữ liệu lớn, logistic lại trở nên mạnh hơn, còn với dữ liệu ít, thì việc khái quát hóa mô hình về một phân phối là một lời giải khá là thông minh.

Naive Bayes

Trước tiên, đáng lẽ phải nói đầu bài viết, chúng ta cần tôn vinh tài tử toán học Bayes, vì những điều tuyệt vời ông đã làm cho ngành xác xuất.

Trong GDA, dữ liệu là liên tục (real-valued vector), bây giờ, chúng ta sẽ tìm hiểu về một thuật toán học khác, với dữ liệu rời rạc (discrete-value).

Naive Bayes thường được sử dụng với việc phân loại text, như vấn đề phân loại emaii rác sử dụng machine learning (text-classification).

Để mô hình một xi (email), chúng ta dùng một vector, độ dài vector là độ dài từ điển, nếu phần tử thứ i xuất hiện thì giá trị là 1, ngược lại là 0.

Một vấn đề ở đây là tính toán, với một từ điển với 50000 từ, sẽ có bao nhiêu khả năng, đó là 2 mũ 50000, 1 con số lớn tới nỗi người ta sẽ chẳng bao giờ tưởng tượng được ra (10^80 là số nguyên tử trong vũ trụ này).

Cách tiếp cận khác, với mỗi một từ trong feature, chúng ta sẽ tính xác xuất xảy ra của nó, và vì các xác xuất này liên quan đến nhau, khi biết được xác xuất từ đầu tiên, ta phải dựa vào nó để tính xác xúât từ thứ 2.

Đẳng thức đầu tiên là thuộc tính thông thường của xác xuất, đẳng thức thứ 2 là Naive Bayes cho rằng, và nó là một sự cho rằng cực kỳ mạnh mẽ, để ta có thể áp dụng cho các thuật toán về sau.

Chúng ta có hàm join-likelihood như sau:

Tương đương với:

Ta tính được:

Đến đây, bài viết xin được dừng lại, còn có 1 số giải pháp giúp tối ưu naive bayes, như laplace smoothing, do hạn chế của mình, sẽ đề cập đến nếu có thời gian và đủ khả năng sau.