Mạng CNN và nhận diện biểu cảm khuôn mặt con người

Mở đầu

Trong bài viết này, mình sẽ nói tổng quan về học máy, nạng noron là gì, mạng noron tích chập là gì, cũng như ứng dụng nó để xây dựng 1 mô hình nhận diện biểu cảm con người.

Tổng quan về học máy

Deep learning là một tập con của lĩnh vực nghiên cứu về trí tuệ nhân tạo (AI) và thuộc nhóm học có giám sát đã giúp máy tính làm những việc tưởng như là không thể trong thập kỉ trước như phân loại hàng ngàn vật thể trong bức ảnh, tự tạo chú thích cho ảnh, bắt trước giọng nói, hay thậm chí sán tác tác phẩm nghệ thuật. Sử dụng mạng lưới thần kinh với nhiều lớp, qua các lớp, mạng phân tích đặc trưng của dữ liệu và đưa ra dự đoán kết quả, liên tục lặp lại quá trình trên tập đào tạo.

Với mỗi nút trên mạng noron là một hàm số được gọi là hàm kích hoạt (activation function), được tính lần lượt theo công thức dưới đây:

$z^{\left(i\right)}=w^Tx^{\left(i\right)}+b$

${\hat{y}}^{\left(i\right)}=a^{\left(i\right)}=sigmoid\left(z^{\left(i\right)}\right)$ .

Với $x^{\left(i\right)}$ là dữ liệu được đưa vào, ma trận w và b được khởi tạo ngẫu nhiên ban đầu và quá trình học của model sẽ là quá trình tìm các tham số của ma trận w và b sao cho với đầu vào là dữ liệu, đầu ra sẽ trả về kết quả đúng như nhãn đã được gắn sẵn $y^{\left(i\right)}$.

- Hàm kích hoạt ở ví dụ trên đây là hàm sigmod, còn có nhiều hàm kích hoạt khác nhau tuỳ thuộc vào kết quả muốn có, xu hướng gần đây hay sử dụng hàm relu làm hàm kích hoạt ở các lớp trung gian cho lĩnh vực nhận diện hình ảnh. - Để biết được kết quả dự đoán của model và kết quả thật sự khác nhau thế nào, ta định nghĩa hàm lỗi cross-entropy theo một quy tắc nào đó, giả sử được định nghĩa sau đây:

$L\left(a^{\left(i\right)},y^{\left(i\right)}\right)=-y^{\left(i\right)}\log{\left(a^{\left(i\right)}\right)}-\left(1-y^{\left(i\right)}\right)\log{\left(1-a^{\left(i\right)}\right)}$

- Hàm L (loss function) trả về một số thực không âm thể hiện độ chênh lệnh giữa giá trị dự đoán và giá trị thực tế, tất nhiên ta luôn muốn tối thiểu hoá hàm lỗi, vì vậy, quá trình đào tạo model là quá trình thay đổi tham số để giảm thiểu giá trị của hàm lỗi. - Hàm lỗi trên toàn bộ giữa liệu được gọi là hàm giá trị (cost function), công thức được thể hiện như sau:

$J=\frac{1}{m}\sum_{i=1}^{m}\mathcal{L}\left(a^{\left(i\right)},y^{\left(i\right)}\right)$

- Để có thể cập nhật, thay đổi giá trị của các tham số W và b sao cho hàm lỗi giảm dần, ta dùng thuật toán gradient denscent, qua vô số các vòng lặp, mỗi lần lặp ta sẽ đi ngược lại hướng tăng của hàm lỗi phía trên bằng cách cập nhật lại W và b cộng hay trừ một lượng nào đó theo hệ số gọi là learning rate alpha.

$W^{\left[l\right]}=W^{\left[l\right]}-\alpha\mathrm{\ }dW^{\left[l\right]}$

$b^{\left[l\right]}=b^{\left[l\right]}-\alpha\mathrm{\ }db^{\left[l\right]}$

- Quá trình tìm ra được dW và db dựa vào một thuật toán gọi là backpropagation, dịch ra tiếng Việt là lan truyền ngược, ngược lại của bước forwardpropagation, bước tính toán ra giá trị hàm lỗi.

- Quá trình lan truyền ngược được tiến hành dựa trên một quy tắc đạo hàm gọi là chain rule sau đây:

$\frac{\partial f}{\partial y}=\ \frac{\partial f}{\partial q}\frac{\partial q}{\partial y}$

- Hình ảnh dưới đây mô phỏng lại quá tình lan truyền xuôi và lan truyền ngược:

- Như vậy, ta tính được dW và db, từ đó cập nhật được giá trị phù hợp cho W và b:

$dW^{\left[l\right]}=\frac{\partial\mathcal{L}}{\partial W^{\left[l\right]}}$

$db^{\left[l\right]}=\frac{\partial\mathcal{L}}{\partial b^{\left[l\right]}}$

- Quá trình lan truyền ngược sẽ cập nhật lại model từ nút cuối cùng đến nút ban đầu lần lượt, với mỗi nút có thể được biểu thị như sau:

- Như vậy, trong mạng noron, quá trình đào tạo được diễn ra như sau:
+ Bước 1: Lấy một tập dữ liệu huấn luyện.
+ Bước 2: Thực thi lan truyền xuôi để lấy được giá trị hàm lỗi.
+ Bước 3: Lan truyền ngược lỗi để lấy được gradient độ dốc (chính là đạo hàm).
+ Bước 4: Sử dụng gradients để cập nhật trọng số của mạng.

Mạng noron tích chập CNN

- Thực tế với dữ liệu là ảnh, không thể áp dụng được mạng noron truyền thống ở trên vì lượng tham số quá lớn, ảnh hưởng nặng nề tới tốc độ học của chương trình, vì thế, trong lĩnh vực thị giác máy tính, có một mạng được đặc trưng bởi phép tích chập ta có thể giải quyết được vấn đề lượng lớn tham số mà vẫn trích xuất ra được đặc trưng của ảnh gọi là CNN, mạng noron tích chập được cấu thành bởi các tầng sau:

- Trước tiên, phép tích chập trên một ảnh là phép trượt một ma trận 2 chiều kenel đặt tại vị trí bên trên trái của ma trận ảnh đã cho rồi thực hiện phép nhân theo từng phần tử trong 2 ma trận, kết quả là lấy tổng của tất cả phép nhân đó, thuật toán được thực hiện cụ thể như dưới đây là phép tích chập trên ảnh X với bộ lọc kenel K:

def corr2d(X, K):

    h, w = K.shape

    Y = np.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))

    for i in range(Y.shape[0]):

        for j in range(Y.shape[1]):

            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()

    return Y

- Với ảnh màu có tới 3 kênh RGB, nên khi biểu diễn ma trận ảnh cũng là ma trận 3 chiều, mỗi kenel cũng là 3 chiều kích thước k*k*3. - Tầng tích chập là đặc trưng của mạng CNN, sử dụng các bộ lọc (filter) có thể học được và phép tích chập để trích xuất đặc trưng của ảnh, được gọi là feature map, ví dụ dưới đây là một bộ lọc trích xuất cạnh dọc của một ảnh.

- Như vậy, filter chính là khả năng “nhìn” của mạng, trích xuất các đặc trưng của ảnh tương tự như mắt người, việc học trong mạng CNN là việc đi tìm ra bộ lọc phù hợp với đặc trưng của bài toán. - Tầng pooling thường được xử dụng sau tầng tích chập, dùng để giảm kích thước mô hình cũng như giảm đi mọt phần lớn tham số trong mạng, do đó cũng kiểm soát tình trạng quá khớp sẽ được nói ở phía dưới đề tài, tầng pooling là tầng không có tham số sinh thêm, có hai dạng phổ biến là max pooling bảo toàn các đặc trưng đã phát hiện, average pooling.

- Tầng kết nối đầy đủ nhận đầu vào là các dữ liệu đã được làm phẳng (flatten) mà mỗi đầu vào kết nối đến tất cả noron của lớp cuối cùng. Trong mô hình mạng CNN, tầng này thường xuất hiện ở cuối mạng. - Một số khái niệm khác trong mạng như strike, padding trong đó strike là bước nhảy của bộ lọc trên khối đầu vào activation map trước nó, mặc định trong ví dụ về phép tích chập ở trên là stride=1, padding có thể hiểu như vùng đệm đầu vào trước đó, nó thường được dùng để điều chỉnh kích cỡ của khối đầu ra. - Công thức để tính khối đầu ra cho lớp tích chập: W1xH1xD1
+ Gọi K là số filter, tức chiều sâu của khối tích chập
+ F là kích thước của filter, ví dụ 3x3
+ S là bước nhảy stride
+ P là tham số padding
Kích cỡ đầu ra W2xH2xD2 được tính theo công thức:

$ W2\ =\ \frac{W1\ -\ F\ +\ 2P}{S}\ +\ 1 $

$ H2\ =\ \frac{H1\ -\ F\ +\ 2P}{S}\ +\ 1 $

$ D2\ =\ K $

Mỗi noron trong tập W2xH2xD2 kết nối với một vùng có kích thước FxFxK. - Để hiểu hơn về kiến trúc này, ta có thể xem qua một kiến trúc đơn giản đầy đủ các phần đã kể trên của mạng CNN:

- Như vậy, các noron trong mạng CNN không kết nối hoàn toàn với các noron trước đó mà chỉ kết nối một phần gọi là trường thụ cảm (receptive field) như trong hình vẽ dưới đây:

- Việc tất cả các noron trong cùng một lớp cùng một toạ độ đều cùng chỉ kết nối đến một phần của đầu vào trước đó làm giảm đáng kể lượng tham số mô hình, và đó cũng là một đặc trưng của mạng norron tích chập.

Tập dữ liệu lựa chọn

Lý do dựa chọn tập dữ liệu fer2013 là bởi số lượng dữ liệu cũng như chất lượng gán nhãn đạt độ chính xác cao của nó đã được kiểm chứng nhiều lần. Bộ dữ liệu ban đầu có 7 nhãn cơ bản, tuy nhiên, có nhiều ảnh không phải mặt người, cũng như bị gãn nhãn sai, vì vậy, đề tài này sử dụng bộ dữ liệu 2013 nhưng sử dũng nhãn được microsoft gán lại, có thêm 1 biểu cảm khuôn mặt, cũng như loại bỏ ảnh không liên quan tới biểu cảm con người. Vì microsoft chỉ cung cấp file csv chứa tên file và nhãn mới nên ta cần viết chương trình để chia các file vào các thư mục khác nhau phục vụ cho mục đích học của model sau này:

    def copy_image(self):

        for od, pd in self.fer_dirs.items():

            src = os.path.join(self.image, pd)

            dst = os.path.join(self.dst, od)

            with open(os.path.join(self.label, pd, 'label.csv')) as f:

                lines = csv.reader(f)

                for line in lines:

                    img,_,n,h,s,sad,a,ds,fear,c,_,_=line

                    if img:

                        arr = [n,h,s,sad,a,ds,fear,c]

                        m = max(arr)

                        idx = arr.index(m)

                        em = ferplus_em[idx]

                        i = fer2013_em.index(em) if em != 'contempt' else 

                        shutil.copyfile(os.path.join(src, img), os.path.join(dst, str(i), img))

Dưới đây là bảng so sánh giữa bộ dữ liệu FER(trên) và FER+(dưới):

Bộ dữ liệu FER+ bao gồm 28273 bức ảnh tập đào tạo (train), 3534 bức ảnh tập xác minh và 3579 bức ảnh thuộc tập kiểm thử độc lập, phân bổ theo đồ thị sau:

Xây dựng model

Hàm softmax

Vì đây là bài toán phân loại, bên cạnh SVM (Support Vector Machine), hàm softmax thường được chọn để đưa ra kết quả dự đoán. Được định nghĩa như sau:

$\sigma\left(z\right)_j=\frac{e^{z_j}}{\sum_{k=1}^{K}e^{z_j}}$

Minibatch

Khác với Batch gradient descent, Mini-batch là phương pháp dùng 1 lượng dữ liệu vừa đủ trong tập đào tạo để thực hiện bước tính đạo hàm, áp dụng cho những tập dữ liệu lớn.

Áp dụng vào tập dữ liệu FER+, việc tính toán 1 lúc hơn 28000 bức ảnh là rất lâu, vì vậy,trong quá trình đào tạo model chọn BatchSize=16.

Tránh hiện tượng overfiting

Hiện tượng overfitting là hiện tượng mà mô hình tìm được quá khớp với dữ liệu đào tạo (training), việc quá khớp này có thể dẫn đến việc dự đoán nhầm, nhiễu, và chất lượng mô hình không còn tốt trên tập kiểm tra nữa, vì vậy, để tránh hiện tượng quá khớp, ta áp dụng một số phương pháp vào mô hình:

Dropout

Trong quá trình training, khi thực hiện bước lan truyền xuôi, đến layer mà có dropout, nó sẽ tắt ngẫu nhiên một số nút trước đó, sử dụng dropout đã được chứng minh có hiệu quả trong việc tránh tình trạng overfitting với các model hiện đại.

Batch Normalization

Batch Normalization đưa dữ liệu về phân phối chuẩn Zero Mean (trung bình bằng không và phương sai đơn vị), việc đưa về phân phối chuẩn giúp đặc trưng về độ lớn của dữ liệu sẽ không bị mất đi khi trainning, quá trình trainning sẽ diễn ra nhanh hơn. Ta có, với mỗi mini-batch (lô nhỏ) có giá trị đầu vào gọi là $B = {x_{i...m}}$, tính trung bình và phương sai trên đó:

$\mu_{B\ }=\ \frac{1}{m}\ \sum_{i=1}^{m}x_i$

${\partial_B^2}_\ =\ \frac{1}{m}\ \sum_{i=1}^{m}{(x_i-\ \mu_{B\ })}^2$

Tiến hành chuẩn hoá các x_i :

${\hat{x}}_{i\ }=\ \frac{x_i-\ \mu_{B\ }}{\sqrt{\partial_B^2\ +\ \in}}$

Tham số $\in$ rất nhỏ được thêm vào để tránh phép chia 0. Đầu ra sau khi chuẩn hoá là:

$y_{i\ }=\ \gamma{\hat{x}}_{i\ }\ +\ \beta$

Với gamma và beta là hai tham số cần học trong suốt quá trình training, vì vậy ở bước gradient denscent, cần tính đạo hàm của gamma và beta rồi cập nhật.

Early stopping, checkpoint

Thực tế cho thấy, khi epochs (số lần lặp lại tất cả dữ liệu của tập đào tạo) quá lớn, độ chính xác với tập kiểm tra bị giảm đi, như vậy, để khắc phục tình đạng ta cần tìm một thồi điểm thích hợp để dừng quá trình đào tạo model lại, để thực hiện điều này, cần chia tập dữ liệu thành 3 tập khác nhau là tập huấn luyện, tập kiểm định và tập kiểm tra như đã nói ở trên, trong quá trình đào tạo model, độ chính xác của mô hình liên tục được đánh giá trên tập kiểm tra khi cảm thấy model không còn khả năng cải thiện được nữa, thì dừng sớm để tránh tăng phương sai. Với đề tài này, tham số theo dõi trong quá trình training là monitor=val_accuracy, muốn quá trình đào tạo tìm model có độ chính xác trên tập kiểm định đạt cao nhất, vì nó cũng cùng phân phối trên tập kiểm tra. Model checkpoint thường được sử dụng kèm Early stopping, để cập nhật lại mô hình sau khi hoàn thành 1 epoch, tránh khi quá trình đào tạo bị lỗi không tìm được model.

Lựa chọn thuật toán tối ưu

Trong phần nghiên cứu này sẽ điểm qua các thuật toán tối ưu nhằm tìm kiếm thuật toán phù hợp nhất cho model.

Gradient descent

Gradient descent một thuật toán tối ưu đơn giản, với mỗi lớp của layer thứ l, cập nhật W và b tất cả các nút theo công thức:

$W^{\left[l\right]}=W^{\left[l\right]}-\alpha\mathrm{\ }dW^{\left[l\right]}$

$b^{\left[l\right]}=b^{\left[l\right]}-\alpha\mathrm{\ }db^{\left[l\right]}$

Giả sử chúng ta đang cố tối ưu hoá hàm chi phí có mặt cắt theo trục Ox như dưới đây, chấm đỏ là điểm cực tiểu.

Thuật toán gradient descent dao động lên xuống theo trục Oy nhiều khiến thuật toán tối ưu bị chậm đi, thêm nữa, nếu hàm mất mát có nhiều điểm cực tiểu, có thể thuật toán sẽ không tìm được vị trí nơi giá trị hàm đạt nhỏ nhất.

Gradient descent momentum

Để khắc phục nhược điểm trên của gradient descent, một thuật toán khác áp dụng nguyên lí: trung bình trọng số theo cấp số nhân (Exponentially Weighted Averages) giúp quá trình tìm kiếm điểm global minimum diễn ra nhanh hơn gọi là gradient descent momentum. Với l là số lớp layer của mạng noron, quá trình cập nhật trọng số sẽ diễn ra như sau:

$v_{dW^{\left[l\right]}}=\beta v_{dW^{\left[l\right]}}+\left(1-\beta\right)dW^{\left[l\right]}$

$W^{\left[l\right]}=W^{\left[l\right]}-\alpha v_{dW^{\left[l\right]}}$

$v_{db^{\left[l\right]}}=\beta v_{db^{\left[l\right]}}+\left(1-\beta\right)db^{\left[l\right]}$

$b^{\left[l\right]}=b^{\left[l\right]}-\alpha v_{db^{\left[l\right]}}$

Với hình vẽ về quá trình tiến tới điểm global minimum ở trên, ta sẽ giảm thiểu sự dao động của trục Oy và tăng nhanh sự giao động ở trục Ox, bằng cách áp dụng trung bình trọng số cấp số nhân cho hai giá trị dW và db, thay thế gradient bằng trung bình của các gradient trong quá khứ với số gradient hiệu dụng là \frac{1}{1-\beta} giúp thuật toán hội tụ nhanh hơn.

Thuật toán RMSprop

Gần tương tự như momentum ở trên, thuật toán RMSprop cũng hoạt động dựa trên trung bình trọng số theo cấp số nhân:

$s_{dW^}=\beta\s_{dW^}+\left(1-\beta\right)dW^2$

$s_{db^}=\beta\s_{db^}+\left(1-\beta\right)db^2$

$W\ =\ W\ -\ \propto\frac{dW}{\sqrt{s_{dw\ \ }+\ \in}}$

$b\ =\ b\ -\ \propto\frac{db}{\sqrt{s_{db\ }+\ \in}}$

Với $\in$ là hằng số vô cùng nhỏ thêm vào để tránh trường hợp chia 0. Khi $dW^2$, $db^2$ lớn thì $\sqrt{s_{dw\ \ }+\ \in}, \sqrt{s_{dw\ \ }+\ \in}$ lớn hơn nhiều, vì vậy sẽ giảm thiểu dao động, tương tự, khi $dW^2$, $db^2$ nhỏ thì $\sqrt{s_{dw\ \ }+\ \in}, \sqrt{s_{dw\ \ }+\ \in}$, trong thực tế, dW và dB là 2 tham số có nhiều chiều và khi nó tăng ta sẽ giảm sự dao động của nó, từ đó có thể tăng tham số alpha khiến quá trình tìm ra điểm global minimum sẽ diễn ra nhanh hơn.

Adam

Thuật toán Adam là sự kết hợp giữa các thuật toán đã đề cập trước, mang tính hiệu quả cao đã được thử nghiệm trên nhiều mạng khác nhau. Bước đầu tiên, thuật toán sử dụng tính v và s dựa trên trung bình trọng số cấp số nhân theo gradient.

$v_{dW^{\left[l\right]}}=\beta_1v_{dW^{\left[l\right]}}+\left(1\beta_1\right)\frac{\partial\mathcal{J}}{\partial W^{\left[l\right]}}$

$s_{dW^{\left[l\right]}}=\beta_2s_{dW^{\left[l\right]}}+\left(1\beta_2\right)\left(\frac{\partial\mathcal{J}}{\partial W^{\left[l\right]}}\right)^2$

Tham số $\beta$_1đặc trưng cho thuật toán gradient descent momentum, vì vậy, thường chọn $\beta_1=\ 0.9$, $\beta_2 $đặc trưng cho thuật toán RMSprop, thường chọn $\beta_2=\ 0.999$. Điều này làm cho phương sai di chuyển chậm hơn nhiều so với động lượng, vì vậy, ta cần chuẩn hoá lại thành 2 biến dưới đây:

$v_{dW^{\left[l\right]}}^{corrected}=\frac{v_{dW^{\left[l\right]}}}{1-\left(\beta_1\right)^t}$

$\ s_{dW^{\left[l\right]}}^{corrected}=\frac{s_{dW^{\left[l\right]}}{1\left(\beta_2\right)^t}$

Như vậy, tương tự RMSpops, cập nhật trọng số W:

$W^{\left[l\right]}=W^{\left[l\right]}-\alpha\frac{v_{dW^{\left[l\right]}}^{corrected}}{\sqrt{s_{dW^{\left[l\right]}}^{corrected}}+\varepsilon}$

Kết luận, nếu momentum được ví như một viên bi nặng lăn theo đà thì RMS lại là một viên bi rất nặng có ma sát, kết hợp lại thành Adam, nó dễ dàng vượt qua các điểm local minimum tiến tới global minimum, vì vậy, trong model nhận diện cảm xúc con người cũng lựa chọn sử dụng Adam làm thuật toán tối ưu.

Quá trình xây dựng model

Với các nghiên cứu lý thuyết cần thiết để xây dựng model ở trên, việc thiết kế model tối ưu là một quá trình lặp lại liên tục tuần hoàn từ lên ý tưởng, đào tạo mạng, kiểm tra đến sửa sai. Qua quá trình xem những nhãn mà model dự đoán sai có đặc điểm chung thế nào, áp dụng cách tính độ chệch và phương sai để liên tục mở rộng mô hình, tăng độ chính xác khi có thể, nhưng cũng giảm thiểu hiện tượng overfitting, underfiting, vanishing gradient. Sau cùng, đây là model tối ưu nhất mà đề tài nghiên cứu này tìm được:

Tiển xử lý, làm giàu dữ liệu:

Ta sẽ sử dụng kỹ thuật data augmentation để làm giàu tập dữ liệu hiện có bằng các phép xoay ảnh, dịch trái, dịch phải, phóng to ảnh, đảo ngược ảnh trên tập train, còn dữ nguyên trên tập validation và tập test.

Kiến trúc model

Số lượng tham số: 711.784, trong đó số lượng tham số đào tạo là 708.584.

Các siêu tham số khác

+ Kích cỡ ảnh đầu vào : 48x48x1
+ Tốc độ học: 0.001
+ Momentum: 0.9
+ Batch Size:16
+ Số lượng epoches tối đa: 60/100
+ Patience: 10

Đào tạo mạng

Quá trình đào tạo mạng được hiện thực bằng ngôn ngữ Python, framework tensorflow, keras. Python là ngôn ngữ bậc cao, dễ dùng, thuận tiện, tensorflow là một framework nổi tiếng về huấn luyện model, keras là một API bậc cao chạy trên nền tensorflow, model chủ yếu được huấn luyện thông qua gọi API bậc cao từ keras. Phát hiện vị trí khuôn mặt, sử dụng OpenCV2.

Đánh giá kết quả trên tập dữ liệu:

Với độ chính xác đạt 81.11 trên tập xác minh, dưới đây là ma trận bối rối trên tập xác minh:

Trên tập kiểm định, độ chính xác đạt 80%. Như vậy, không có sự khác biệt quá lớn giữa độ chính xác các tập đào tạo, tập kiểm định và tập xác minh, model hoàn toàn có thể mở rộng hơn nữa.

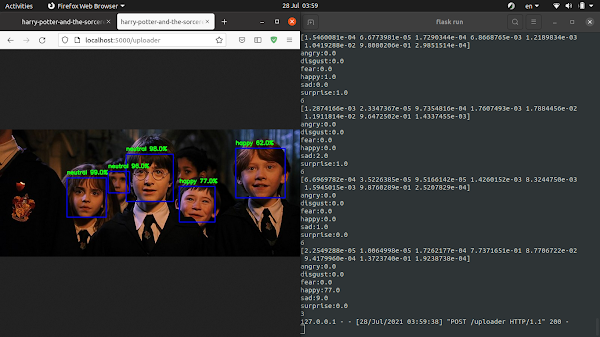
Một số kết quả dự đoán trong thực tế

Ứng dụng thực tế, tạo API, web cho phép nhận diện cảm xúc con người realtime qua camera trước:

Ngôn ngữ backend: python, thư viện frontend: reactjs. Ứng dụng thư viện flask trong python để viết API đơn giản gửi ảnh lên server, ảnh trả về sẽ là ảnh dự đoán. Đầu tiên chúng ta cần dùng thư viện opencv để định vị tất cả khuôn mặt có trong bức ảnh rồi chạy model dự đoán trên đó. Cụ thể như sau:

Do khó khăn trong việc tìm kiếm máy chủ để chạy realtime camera, nên web realtime sẽ được viết trên tensorflowjs, ta chỉ cần convert model về dạng json là xử lý được, thuật toán cũng tương tự như ở trên, nên xin phép sẽ không trình bày lại. Kết quả cuối cùng: model nhận diện nhanh chóng, đạt độ chính xác cao.

Bạn có thể thử dự đoán tại đây (bit.ly/emotion_ai

Source code