Linear Algebra - Đại số tuyến tính cho kỹ sư
Các khái niệm cơ bản và ký hiệu
Đại số tuyến tính giúp viết các tập hợp tuyến tính theo cách nhìn đơn giản hơn ! Ví dụ, xét hệ phương trình sau:
Có thể viết đơn giản lại thành:
Nếu bạn không thấy đơn giản và dễ hiểu hơn cách viết truyền thống, thì chấp nhận đi, đại số tuyến tính giúp viết phương trình tổng quát nhanh hơn, và quan trọng là, giúp máy tính tính toán nhanh hơn.
Một số định nghĩa cơ bản về đại số có thể tóm gọn bằng 1 ví dụ sau:
Nhân ma trận (Matrix Multiplication)
Kết quả của phép nhân ma trận A và B là 1 ma trận C = AB thuộc $R^{mxn}$ nơi mà mỗi phần tử trong ma trận được tính như sau:
Nhân 2 vector (Vector-Vector product)
Cho hai vector x và y thuộc $R^{n}$, kết quả của $x^Ty$ gọi là inner product hay dot product, $x^Ty=y^Ty$:
Cho 2 vector x thuộc $R^m$, y thuộc $R^n$, kêt quả $xy^T$ gọi là outer product, và $(xy^T)_{ij} = x_i y_j$
Một ví dụ hay:
Phép nhân Matrix-Vector (Matrix-Vector Products)
Đây là ví dụ nhân ma trận A và vector x:
Nếu vector x có nhiều phần tử, $y_i={a_i}^Tx$:
Ta nói y là tổ hợp tuyến tính (linear combination) các côt của A trong đó hệ số tuyến tính của tổ hợp tuyến tính là x.
Ta có, $y^T=x^TA$:
Hoặc biến đổi:
$y^T$ là tổ hợp tuyến tính các cột của A.
Nhân ma trận (Matrix-Matrix Products)
Không nói nhiều:
Đây là một loại tích 2 ma trận thứ 2:
Chúng ta có thể xem phép nhân ma trận như một tập tích phép nhân của cacs vector:
Hoạc có thể biển đổi:
Đừng lo nếu bạn không thể biến đổi tinh vi đến vậy, chúng ta chỉ đang tối đa hóa độ lớn của phép nhân ma trận, sau đây là một số tính chất cơ bản của nhân ma trận:
+ (AB)C = A(BC)
+ A(B+C) = AB + AC
+ AB khác BA
Chứng minh các tính chất đó dựa trên định nghĩa của phép nhân ma trận, ví dụ dưới đây:
Toán tử và tính chât
Ma trận đơn vị và ma trận và ma trận đường chéo:
Có thể hiểu đơn giản qua hai công thức sau:
Tính chất của ma trận chuyển vị
Ma trận đối xứng
Nếu $A=A^T$ thì gọi là ma trận đối xứng (Symetric Matrices), nếu $A=-A^T$ thì gọi là ma trận chống đối xứng (anti-symetric).
Với mọi ma trận $A+A^T$ là ma trận đối xứng, $A-A^T$ là ma trận chống dối xứng.
Vết của Matrix (Trace)
Đây là một số tính chất rất quan trọng của trace sẽ được áp dụng trong Machine Learning, bạn nên nhớ:
Một ví dụ về cách chứng minh:
Chuẩn (Norm)
Có thể hiểu norm của 1 vector là 1 cách định nghĩa độ dài của vector đó, và có nhiều cách định nghĩa khác nhau, nên có nhiều chuẩn khác nhau. Ví dụ chuẩn l2-norm:
Chuẩn l1-norm:
Chuẩn $l_{\infty}-norm$
Chuẩn tổng quát $l_p$ norm:
Chuẩn Frobenius:
Hạng của ma trận và độc lập tuyến tính
Một một tập hợp vector {x1,x2,...xn}, ta nói hệ độc lập tuyến tính khi không có vector nào có thể biểu diễn từ các vector khác trong hệ, như vậy, nếu chỉ cần có 1 vector biểu diễn đươc bằng các vector khác trong hệ thì hệ dó là phụ thuộc tuyến tính.
Tổng quát, một hệ phụ thụôc tuyến tính khi:
Ví dụ:
Ta thây: $x_3=-2x_1+x_2$, như vậy, hệ trên là phụ thuộc tuyến tính. Trong machine learning, ta phải luôn đưa hệ về độc lập tuyến tính, vì nếu hệ phụ thuộc tuyên tính tức là có phần tử dư thừa.
Hạng của ma trận là kích thước lớn nhất mà một ma trận độc lập tuyeesnt tính, hay hiểu đơn giản là số cột độc lập tuyến tính của A, một số tính chất như tài liệu dưới dây:
Nghịch đảo ma trạn (The Inverse)
Định nghĩa:
Tính chất:
Ma trận trực giao (Orthogonal matrices)
Nếu các vector trong hệ trực giao $x^Ty=0$ và x theo chuẩn l2 ||x||_2 = 1 thì gọi là ma trận trực giao.
Phạm vi và không gian rỗng của ma trận (Range & Nullspace)
Ta định nghĩa Span của 1 vector là 1 tập hợp tất cả vector có thể biểu diễn bằng 1 tổ hợp tuyến tính của vector đó:
Ta định nghĩa hình chiếu (projection) của một vector y lên span của nó (v) theo công thức sau, được đo bằng chuẩn Euclidean:
Phạm vi (range) hay không gian cột của vector được gọi là R(A) được định nghĩa theo span:
Hình chiếu của vector y trên A:
Khi A chỉ chứa 1 cột a thuộc $R^m$, ta có công thức hình chiếu sau:
Không gian rỗng của ma trận A là một tập hợp các vector bằng 0, ký hiệu N(A):
Công thức liên hệ giữa R($A^T$) và N(A):
Hai tập trên gọi là orthogonal complements.
Định thức (The Determinant)
Định thức đươc tính bằng công thức sau:
Ví dụ:
Quadratic Forms and Positive Semidefinite Matrices
Cho ma trận A và vector x, giá tri vô hướng của $x^TAx$ được gọi là quadratic form:
Giá trị riêng và vector riêng (Eigenvalues và Eigenvectors)
Cho ma trận A, chúng ta nói lamda là 1 giá trị riêng nếu:
Giải tích ma trận (Matrix Calculus)
The Gradient
Gọi hàm f với đầu vào là một ma trận f(A), đạo hàm của f theo A đực tính:
Với môi một phần tử ta tính đạo hàm 1 phần:
Đạo hàm của vector:
Một số tính chât:
The Hesisan
Đạo hàm được định nghĩa như sau:
Đạo hàm hessian luôn luôn đối xứng
Mình xin dừng phần sau tại đây, đến giờ, mình chưa biết ứng dụng các kiến thức đó nên xin tạm không viết tiếp.
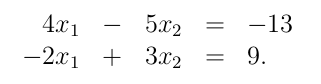










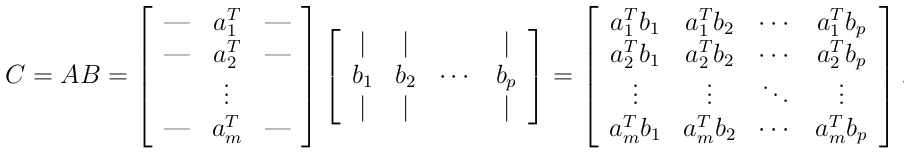









































Nhận xét
Đăng nhận xét