Codeforces Contest: Errich Tac Toe (Hard Version)

 

C2. Errich-Tac-Toe (Hard Version)

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

The only difference between the easy and hard versions is that tokens of type O do not appear in the input of the easy version.

Errichto gave Monogon the following challenge in order to intimidate him from taking his top contributor spot on Codeforces.

In a Tic-Tac-Toe grid, there are n$n$ rows and n$n$ columns. Each cell of the grid is either empty or contains a token. There are two types of tokens: X and O. If there exist three tokens of the same type consecutive in a row or column, it is a winning configuration. Otherwise, it is a draw configuration.

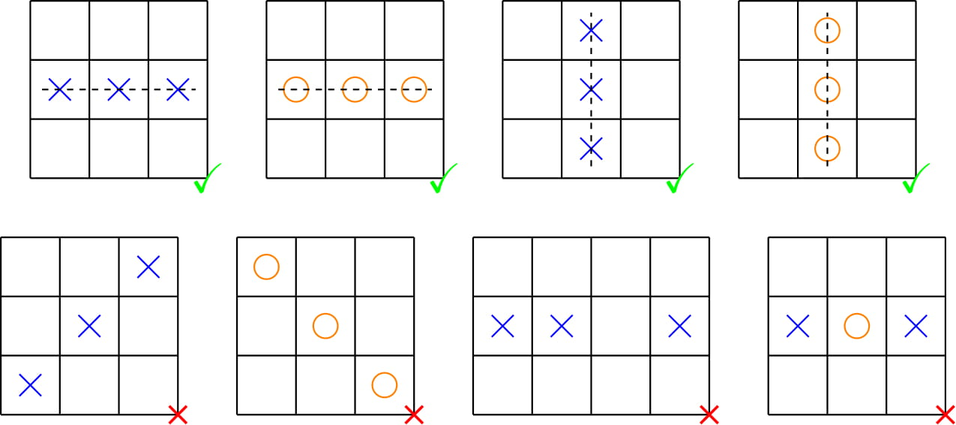The patterns in the first row are winning configurations. The patterns in the second row are draw configurations.

In an operation, you can change an X to an O, or an O to an X. Let k$k$ denote the total number of tokens in the grid. Your task is to make the grid a draw in at most ⌊k3⌋$\lfloor \frac{k}{3}\rfloor$ (rounding down) operations.

You are not required to minimize the number of operations.

Input

The first line contains a single integer t$t$ (1≤t≤100$1\le t\le 100$) — the number of test cases.

The first line of each test case contains a single integer n$n$ (1≤n≤300$1\le n\le 300$) — the size of the grid.

The following n$n$ lines each contain a string of n$n$ characters, denoting the initial grid. The character in the i$i$-th row and j$j$-th column is '.' if the cell is empty, or it is the type of token in the cell: 'X' or 'O'.

It is guaranteed that not all cells are empty.

The sum of n$n$ across all test cases does not exceed 300$300$.

Output

For each test case, print the state of the grid after applying the operations.

We have proof that a solution always exists. If there are multiple solutions, print any.

Example

input

Copy

3
3
.O.
OOO
.O.
6
XXXOOO
XXXOOO
XX..OO
OO..XX
OOOXXX
OOOXXX
5
.OOO.
OXXXO
OXXXO
OXXXO
.OOO.

output

Copy

.O.
OXO
.O.
OXXOOX
XOXOXO
XX..OO
OO..XX
OXOXOX
XOOXXO
.OXO.
OOXXO
XXOXX
OXXOO
.OXO.

Note

In the first test case, there are initially three 'O' consecutive in the second row and the second column. By changing the middle token to 'X' we make the grid a draw, and we only changed 1≤⌊5/3⌋$1\le \lfloor 5/3\rfloor$ token.

In the second test case, the final grid is a draw. We only changed 8≤⌊32/3⌋$8\le \lfloor 32/3\rfloor$ tokens.

In the third test case, the final grid is a draw. We only changed 7≤⌊21/3⌋$7\le \lfloor 21/3\rfloor$ tokens.

Ý tưởng:

Ở bài khó hơn này sự khác biệt duy nhất theo đề nói là có cả O ở trong bộ test, nếu bạn chưa làm phiên bản dễ của bài toán thì nên làm trước khi xem bài viết này. Vì có cả O trong bộ test nên ta không chỉ có các khả năng thay X bằng O như bài cũ mà ta còn có thêm các khả năng thay O bằng X để thỏa mãn điều kiện đề bài.

Tuy nhiên ý tưởng không khác bài toán gốc của ta.

Gọi boardsX[3][n][n] là một vector 3 chiều với boardsX[0], boardsX[1], boardsX[2] là các phương án lấy đường chéo loại 0, loại 1 và loại 2 và thay nó bằng O.

Gọi boardsO[3][n][n] là một vector 3 chiều với boardsO[0], boardsO[1], boardsO[2] là các phương án lấy đường chéo loại 0, loại 1 và loại 2 và thay nó bằng X.

Gọi changesX[3] là số phần tử cần thay đổi cho mỗi phương án boardsX[0], boardsX[1], boardsX[2], và changesO[3] là số phần tử cần thay đổi cho mỗi phương án boardsO[0], boardsO[1], boardsO[2].

Gọi K là số phần tử tối đa cần thay đổi. 

Giờ đây, ta chỉ cần tìm tất cả các khả năng xóa đường chéo X hay O, hay cả X và O là sẽ ra kết quả bài toán bằng tổ hợp và lấy ra trường hợp cần thay đổi ít nhất, lưu ý điều kiện changesX[i]+changesO[j] <=k/3 . ( Chứng minh tương tự bài trước).

Sourcecode tham khảo:  Python: