Codeforces contest: Errich-Tac-Toe (Easy Version)

- tháng 12 08, 2020

Errichto gave Monogon the following challenge in order to intimidate him from taking his top contributor spot on Codeforces.

In a Tic-Tac-Toe grid, there are $n$ rows and $n$ columns. Each cell of the grid is either empty or contains a token. There are two types of tokens: X and O. If there exist three tokens of the same type consecutive in a row or column, it is a winning configuration. Otherwise, it is a draw configuration.

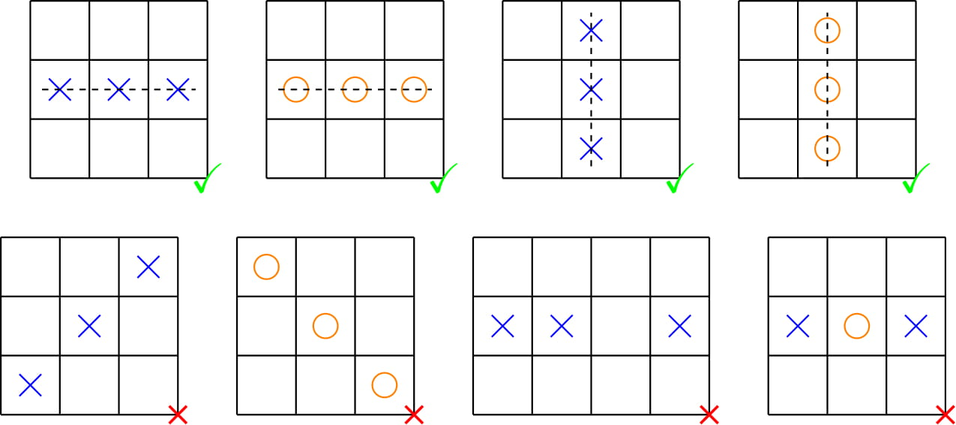$\text{[math]}$ The patterns in the first row are winning configurations. The patterns in the second row are draw configurations.

In an operation, you can change an X to an O, or an O to an X. Let $k$ denote the total number of tokens in the grid. Your task is to make the grid a draw in at most $⌊ \frac{k}{3} ⌋$ (rounding down) operations.

You are not required to minimize the number of operations.

Input

The first line contains a single integer $t$ ( $1 \leq t \leq 100$ ) — the number of test cases.

The first line of each test case contains a single integer $n$ ( $1 \leq n \leq 300$ ) — the size of the grid.

The following $n$ lines each contain a string of $n$ characters, denoting the initial grid. The character in the $i$ -th row and $j$ -th column is '.' if the cell is empty, or it is the type of token in the cell: 'X' or 'O'.

It is guaranteed that not all cells are empty.

In the easy version, the character 'O' does not appear in the input.

The sum of $n$ across all test cases does not exceed $300$ .

Output

For each test case, print the state of the grid after applying the operations.

We have proof that a solution always exists. If there are multiple solutions, print any.

Example
inputCopy
3
3
.X.
XXX
.X.
6
XX.XXX
XXXXXX
XXX.XX
XXXXXX
XX.X.X
XXXXXX
5
XXX.X
.X..X
XXX.X
..X..
..X..
outputCopy
.X.
XOX
.X.
XX.XXO
XOXXOX
OXX.XX
XOOXXO
XX.X.X
OXXOXX
XOX.X
.X..X
XXO.O
..X..
..X..

Note

In the first test case, there are initially three 'X' consecutive in the second row and the second column. By changing the middle token to 'O' we make the grid a draw, and we only changed $1 \leq ⌊ 5 / 3 ⌋$ token.

In the second test case, we change only $9 \leq ⌊ 32 / 3 ⌋$ tokens, and there does not exist any three 'X' or 'O' consecutive in a row or column, so it is a draw.

In the third test case, we change only $3 \leq ⌊ 12 / 3 ⌋$ tokens, and the resulting grid is a draw.

Lời giải:

Giả sử ta có ma trận 5x5 như dưới đây:

0 1 2 3 4

0 X X X X X

1 X X X X X

2 X X X X X

3 X X X X X

4 X X X X X

Để thỏa mãn điểu kiện đề bài là không được 3 ô liên tiếp ngang dọc là 'X' thì ta xét 1 ma trận nhỏ hơn:

0 1 2

0 X X X

1 X X X

2 X X X

Từ (0,0) gọi các đường chéo song song với đường chéo chính lần lượt là 0,1,2,3,4.

Nếu thay 2 đường chéo 0,3 bằng 'O', tốn 3 kí tự

0 1 2

0 O X X

1 X X O

2 X O X

Nếu thay 1,4 bằng 0:

0 1 2

0 X 0 X

1 0 X X

2 X X 0

Nếu thay 2 bằng 0:

0 1 2

0 X X O

1 X 0 X

2 O X X

Như vậy, hoàn toàn thỏa mãn điều kiện đề bài nếu ta xóa 1 trong 3 đường chéo liền kề nhau. Gọi 3 đường chéo liền kề là 0,1,2, để biết phần tử (x,y) nằm ở nhóm đường chéo nào ta có (x+y)%3.

Gọi số phần tử cần thay đổi là changes, ta có : changes[0]+changes[1]+changes[2] = K

Vậy: min(changes[0],changes[1],changes[2]) <= K/3

Gọi boards[3][n][n] là một vector 3 chiều, trong đó boards[0] tức để xóa hết đường chéo loại 0.

Bài toán trở nên đơn giản như dưới đây:

Nhận xét

Nặc danhlúc 17:00 19 tháng 10, 2023
public class LineIntersection {
public static boolean doIntersect(Line line1, Line line2) {
double x1 = line1.start.x;
double y1 = line1.start.y;
double x2 = line1.end.x;
double y2 = line1.end.y;

double x3 = line2.start.x;
double y3 = line2.start.y;
double x4 = line2.end.x;
double y4 = line2.end.y;

// Tính các hệ số cho phương trình đường thẳng của line1 (Ax + By = C)
double A1 = y2 - y1;
double B1 = x1 - x2;
double C1 = A1 * x1 + B1 * y1;

// Tính các hệ số cho phương trình đường thẳng của line2 (Ax + By = C)
double A2 = y4 - y3;
double B2 = x3 - x4;
double C2 = A2 * x3 + B2 * y3;

// Tính điểm giao nhau (x, y) bằng cách giải hệ phương trình
double determinant = A1 * B2 - A2 * B1;

if (determinant == 0) {
// Hai đường thẳng là song song hoặc trùng nhau
return false;
} else {
double intersectX = (B2 * C1 - B1 * C2) / determinant;
double intersectY = (A1 * C2 - A2 * C1) / determinant;

// Kiểm tra xem điểm giao nằm trong khoảng của cả hai đoạn thẳng
return isBetween(x1, x2, intersectX) && isBetween(x3, x4, intersectX) &&
isBetween(y1, y2, intersectY) && isBetween(y3, y4, intersectY);
}
}

public static boolean isBetween(double a, double b, double c) {
return c >= Math.min(a, b) && c <= Math.max(a, b);
}

// Các phần còn lại của lớp và hàm main giữ nguyên từ ví dụ trước

public static void main(String[] args) {
// ... (giữ nguyên phần khai báo điểm A, B, C, D và đoạn thẳng AB, CD từ ví dụ trước)
// ... (sử dụng hàm doIntersect để kiểm tra xem đoạn AB và CD cắt nhau hay không)
}
}
Trả lờiXóa
Trả lời
Nặc danhlúc 19:30 19 tháng 10, 2023
class Point {
double x, y;

public Point(double x, double y) {
this.x = x;
this.y = y;
}
}

class Circle {
Point center;
double radius;

public Circle(Point center, Point X) {
this.center = center;
this.radius = Math.sqrt((X.x - center.x) * (X.x - center.x) + (X.y - center.y) * (X.y - center.y));
}

public boolean doesIntersectWithLine(Point A, Point B) {
double Ax = A.x;
double Ay = A.y;
double Bx = B.x;
double By = B.y;

double Ox = center.x;
double Oy = center.y;

double r = radius;

double d1 = (Ax - Ox) * (Ax - Ox) + (Ay - Oy) * (Ay - Oy);
double d2 = (Bx - Ox) * (Bx - Ox) + (By - Oy) * (By - Oy);
double rSquared = r * r;

if ((d1 < rSquared && d2 > rSquared) || (d1 > rSquared && d2 < rSquared)) {
return true; // Đoạn AB cắt đường tròn.
} else if (d1 <= rSquared && d2 <= rSquared) {
return false; // Cả đoạn AB nằm trong đường tròn.
} else {
// Kiểm tra điểm A và B có nằm ở hai bên của đường tròn hoặc ở cùng một bên.
double distanceToA = Math.sqrt(d1);
double distanceToB = Math.sqrt(d2);

return (distanceToA < r && distanceToB < r) || (distanceToA > r && distanceToB > r);
}
}
}

public class CircleLineIntersection {
public static void main(String[] args) {
Point A = new Point(1, 1);
Point B = new Point(4, 4);
Point O = new Point(3, 3); // Tâm đường tròn
Point X = new Point(3, 4); // Một điểm trên đường tròn

Circle circle = new Circle(O, X);

if (circle.doesIntersectWithLine(A, B)) {
System.out.println("Đoạn AB cắt đường tròn.");
} else {
System.out.println("Đoạn AB không cắt đường tròn.");
}
}
}
Trả lờiXóa
Trả lời
Nặc danhlúc 20:28 19 tháng 10, 2023
public boolean doesIntersectWithLine(Point A, Point B) {
double Ox = center.x;
double Oy = center.y;
double r = radius;

// Tính khoảng cách từ tâm đường tròn đến đoạn AB
double distance = Math.abs((B.x - A.x) * (A.y - Oy) - (A.x - Ox) * (B.y - A.y))
/ Math.sqrt(Math.pow(B.x - A.x, 2) + Math.pow(B.y - A.y, 2));

// Kiểm tra xem khoảng cách này có nhỏ hơn bán kính của đường tròn không
if (distance <= r) {
return true; // Đoạn AB cắt đường tròn.
}

return false; // Đoạn AB không cắt đường tròn.
}
}

public class CircleLineIntersection {
public static void main(String[] args) {
Point A = new Point(1, 1);
Point B = new Point(4, 4);
Point O = new Point(3, 3); // Tâm đường tròn
Point X = new Point(3, 4); // Một điểm trên đường tròn

Circle circle = new Circle(O, X);

if (circle.doesIntersectWithLine(A, B)) {
System.out.println("Đoạn AB cắt đường tròn.");
} else {
System.out.println("Đoạn AB không cắt đường tròn.");
}
}
}
Trong ví dụ này, chúng ta tính bán kính của đường tròn dựa trên tâm và một điểm trên đường tròn (X). Sau đó, chúng ta sử dụng phương trình đường tròn để kiểm tra xem đoạn AB có cắt đường tròn không bằng cách tính khoảng cách từ tâm đường tròn đến đoạn AB và so sánh với bán kính của đường tròn.

Trả lờiXóa
Trả lời
Nặc danhlúc 15:59 20 tháng 10, 2023
RectF rectF = new RectF(left, top, right, bottom);

// Tạo đoạn thẳng LEFT từ (left, top) đến (left, bottom)
PointF leftStart = new PointF(rectF.left, rectF.top);
PointF leftEnd = new PointF(rectF.left, rectF.bottom);

// Tạo đoạn thẳng RIGHT từ (right, top) đến (right, bottom)
PointF rightStart = new PointF(rectF.right, rectF.top);
PointF rightEnd = new PointF(rectF.right, rectF.bottom);

// Tạo đoạn thẳng TOP từ (left, top) đến (right, top)
PointF topStart = new PointF(rectF.left, rectF.top);
PointF topEnd = new PointF(rectF.right, rectF.top);

// Tạo đoạn thẳng BOTTOM từ (left, bottom) đến (right, bottom)
PointF bottomStart = new PointF(rectF.left, rectF.bottom);
PointF bottomEnd = new PointF(rectF.right, rectF.bottom);

// Bây giờ bạn có bốn đoạn thẳng LEFT, RIGHT, TOP, và BOTTOM
Trả lờiXóa
Trả lời
Nặc danhlúc 16:44 20 tháng 10, 2023
float startX, startY; // Store the initial touch coordinates
float endX, endY; // Store the final touch coordinates

// Handle the onTouchMove event
@Override
public boolean onTouchEvent(MotionEvent event) {
switch (event.getAction()) {
case MotionEvent.ACTION_DOWN:
startX = event.getX();
startY = event.getY();
break;

case MotionEvent.ACTION_MOVE:
endX = event.getX();
endY = event.getY();

float deltaX = endX - startX;
float deltaY = endY - startY;

if (Math.abs(deltaX) > Math.abs(deltaY)) {
if (deltaX > 0) {
// Move to the right
} else {
// Move to the left
}
} else {
if (deltaY > 0) {
// Move downwards
} else {
// Move upwards
}
}

startX = endX;
startY = endY
Trả lờiXóa
Trả lời

Thêm nhận xét

Tìm kiếm Blog này

Le Quang Duy

Codeforces contest: Errich-Tac-Toe (Easy Version)

Nhận xét

Đăng nhận xét

Bài đăng phổ biến từ blog này

Hiểu về Norm Regularization

Mạng CNN và nhận diện biểu cảm khuôn mặt con người

Những thuật toán nền tảng trong lĩnh vực Trí tuệ nhân tạo (Artificial Intelligence I)