Solutions Problems October
Cũng gần 3 tháng rồi mình chưa bắt đầu lại thói quen này, viết vậy đủ hiểu độ trì của bản thân.
Minimum Number of Arrows to Burst Balloons
There are some spherical balloons spread in two-dimensional space. For each balloon, provided input is the start and end coordinates of the horizontal diameter. Since it's horizontal, y-coordinates don't matter, and hence the x-coordinates of start and end of the diameter suffice. The start is always smaller than the end.
An arrow can be shot up exactly vertically from different points along the x-axis. A balloon with xstart and xend bursts by an arrow shot at x if xstart ≤ x ≤ xend. There is no limit to the number of arrows that can be shot. An arrow once shot keeps traveling up infinitely.
Given an array points where points[i] = [xstart, xend], return the minimum number of arrows that must be shot to burst all balloons.
Example 1:
Input: points = [[10,16],[2,8],[1,6],[7,12]] Output: 2 Explanation: One way is to shoot one arrow for example at x = 6 (bursting the balloons [2,8] and [1,6]) and another arrow at x = 11 (bursting the other two balloons).
Example 2:
Input: points = [[1,2],[3,4],[5,6],[7,8]] Output: 4
Example 3:
Input: points = [[1,2],[2,3],[3,4],[4,5]] Output: 2
Example 4:
Input: points = [[1,2]] Output: 1
Example 5:
Input: points = [[2,3],[2,3]] Output: 1
Constraints:
0 <= points.length <= 104points.length == 2-231 <= xstart < xend <= 231 - 1
In a row of dominoes, A[i] and B[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)
We may rotate the ith domino, so that A[i] and B[i] swap values.
Return the minimum number of rotations so that all the values in A are the same, or all the values in B are the same.
If it cannot be done, return -1.
Example 1:
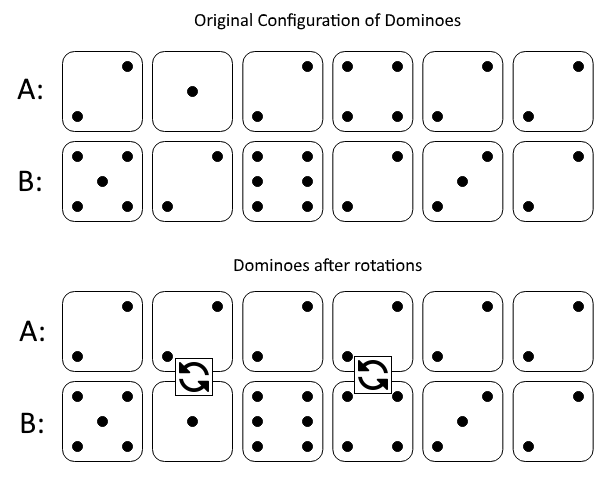
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2] Output: 2 Explanation: The first figure represents the dominoes as given by A and B: before we do any rotations. If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.
Example 2:
Input: A = [3,5,1,2,3], B = [3,6,3,3,4] Output: -1 Explanation: In this case, it is not possible to rotate the dominoes to make one row of values equal.
Constraints:
2 <= A.length == B.length <= 2 * 1041 <= A[i], B[i] <= 6
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.
class Node {
public int val;
public List<Node> neighbors;
}
Test case format:
For simplicity sake, each node's value is the same as the node's index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.
Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
Example 1:
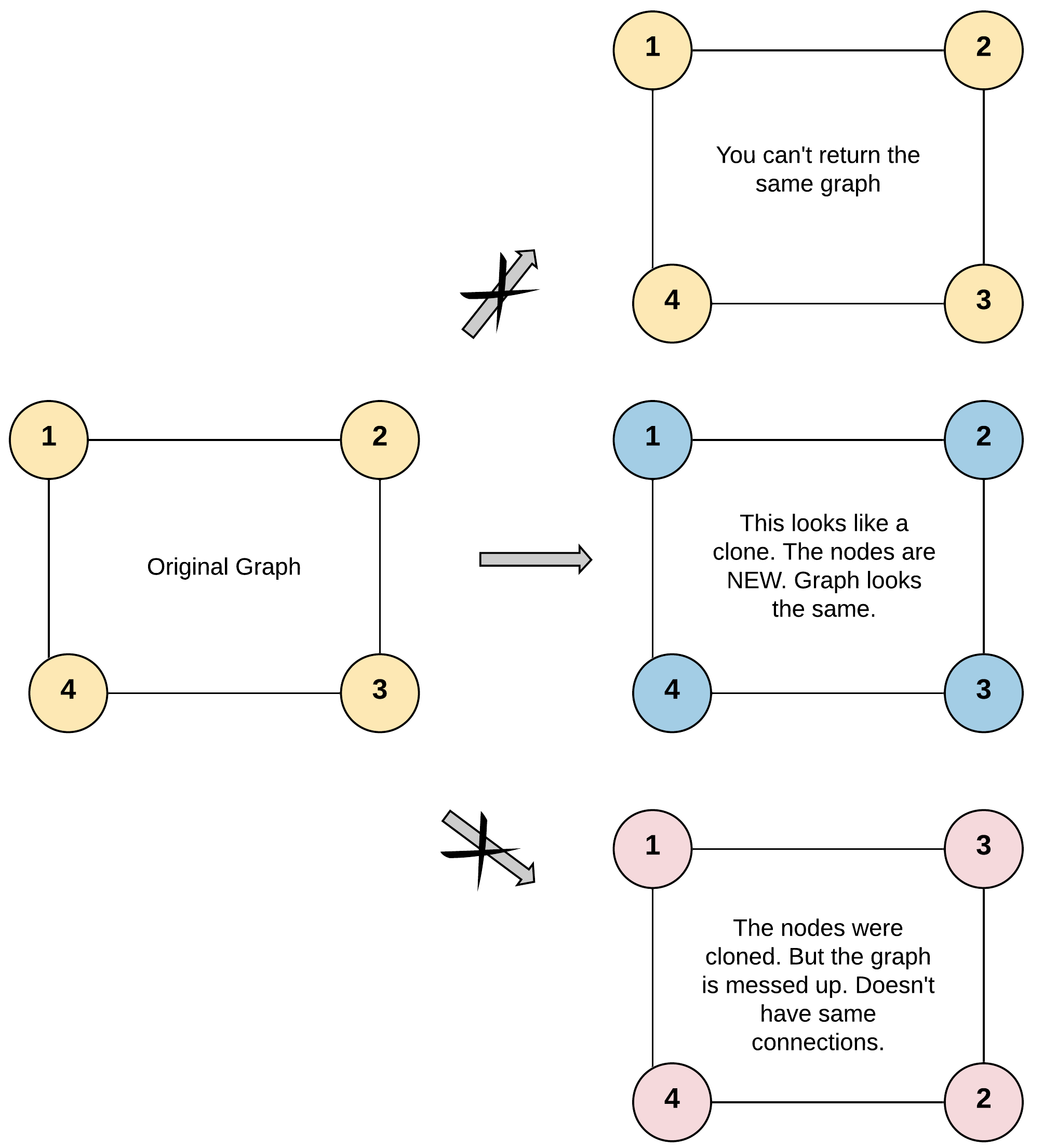
Input: adjList = [[2,4],[1,3],[2,4],[1,3]] Output: [[2,4],[1,3],[2,4],[1,3]] Explanation: There are 4 nodes in the graph. 1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4). 2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3). 3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4). 4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
Example 2:
Input: adjList = [[]] Output: [[]] Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
Example 3:
Input: adjList = [] Output: [] Explanation: This an empty graph, it does not have any nodes.
Example 4:
Input: adjList = [[2],[1]] Output: [[2],[1]]
Constraints:
1 <= Node.val <= 100Node.valis unique for each node.- Number of Nodes will not exceed 100.
- There is no repeated edges and no self-loops in the graph.
- The Graph is connected and all nodes can be visited starting from the given node.
We are given an array asteroids of integers representing asteroids in a row.
For each asteroid, the absolute value represents its size, and the sign represents its direction (positive meaning right, negative meaning left). Each asteroid moves at the same speed.
Find out the state of the asteroids after all collisions. If two asteroids meet, the smaller one will explode. If both are the same size, both will explode. Two asteroids moving in the same direction will never meet.
Example 1:
Input: asteroids = [5,10,-5] Output: [5,10] Explanation: The 10 and -5 collide resulting in 10. The 5 and 10 never collide.
Example 2:
Input: asteroids = [8,-8] Output: [] Explanation: The 8 and -8 collide exploding each other.
Example 3:
Input: asteroids = [10,2,-5] Output: [10] Explanation: The 2 and -5 collide resulting in -5. The 10 and -5 collide resulting in 10.
Example 4:
Input: asteroids = [-2,-1,1,2] Output: [-2,-1,1,2] Explanation: The -2 and -1 are moving left, while the 1 and 2 are moving right. Asteroids moving the same direction never meet, so no asteroids will meet each other.
Constraints:
1 <= asteroids <= 104-1000 <= asteroids[i] <= 1000asteroids[i] != 0



Nhận xét
Đăng nhận xét