MayChalenge (53-54-55-56-57-58)

Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

(Formally, a closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.  The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval.  For example, the intersection of [1, 3] and [2, 4] is [2, 3].)

Example 1:

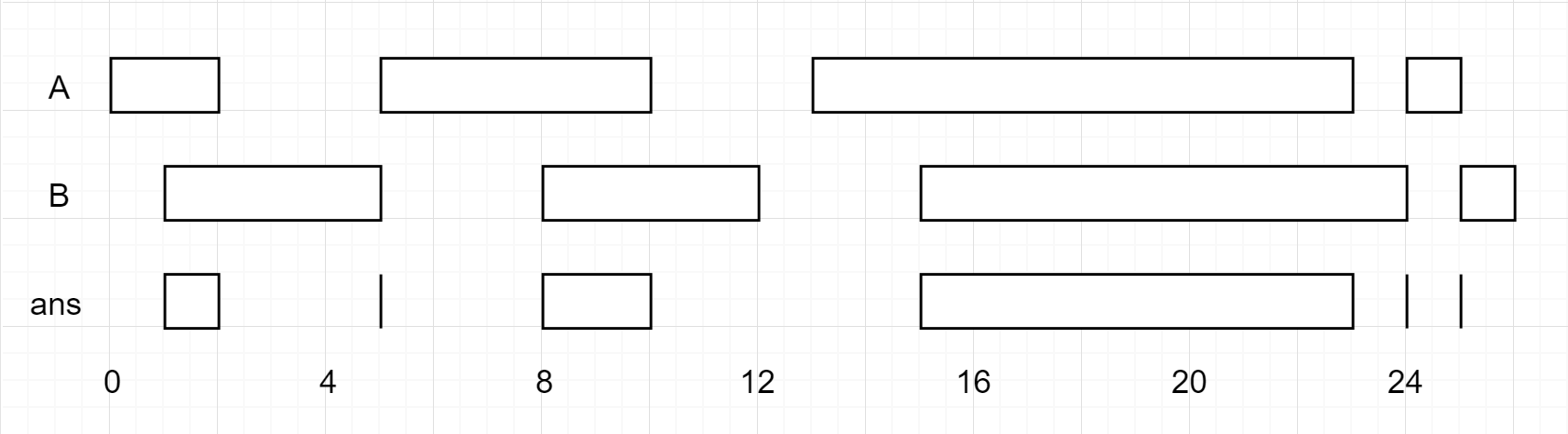
Input: A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Note:

1. 0 <= A.length < 1000
2. 0 <= B.length < 1000
3. 0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9

I am busy, so i only show my code, the explain will coming:

Return the root node of a binary search tree that matches the given preorder traversal.

(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val.  Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.)

It's guaranteed that for the given test cases there is always possible to find a binary search tree with the given requirements.

Example 1:

Input: [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]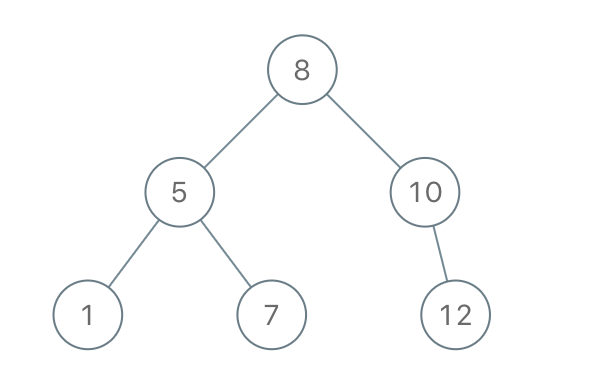

Constraints:

• 1 <= preorder.length <= 100
• 1 <= preorder[i] <= 10^8
• The values of preorder are distinct.

This problem i posted.

We write the integers of A and B (in the order they are given) on two separate horizontal lines.

Now, we may draw connecting lines: a straight line connecting two numbers A[i] and B[j] such that:

• A[i] == B[j];
• The line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting lines cannot intersect even at the endpoints: each number can only belong to one connecting line.

Return the maximum number of connecting lines we can draw in this way.

Example 1:

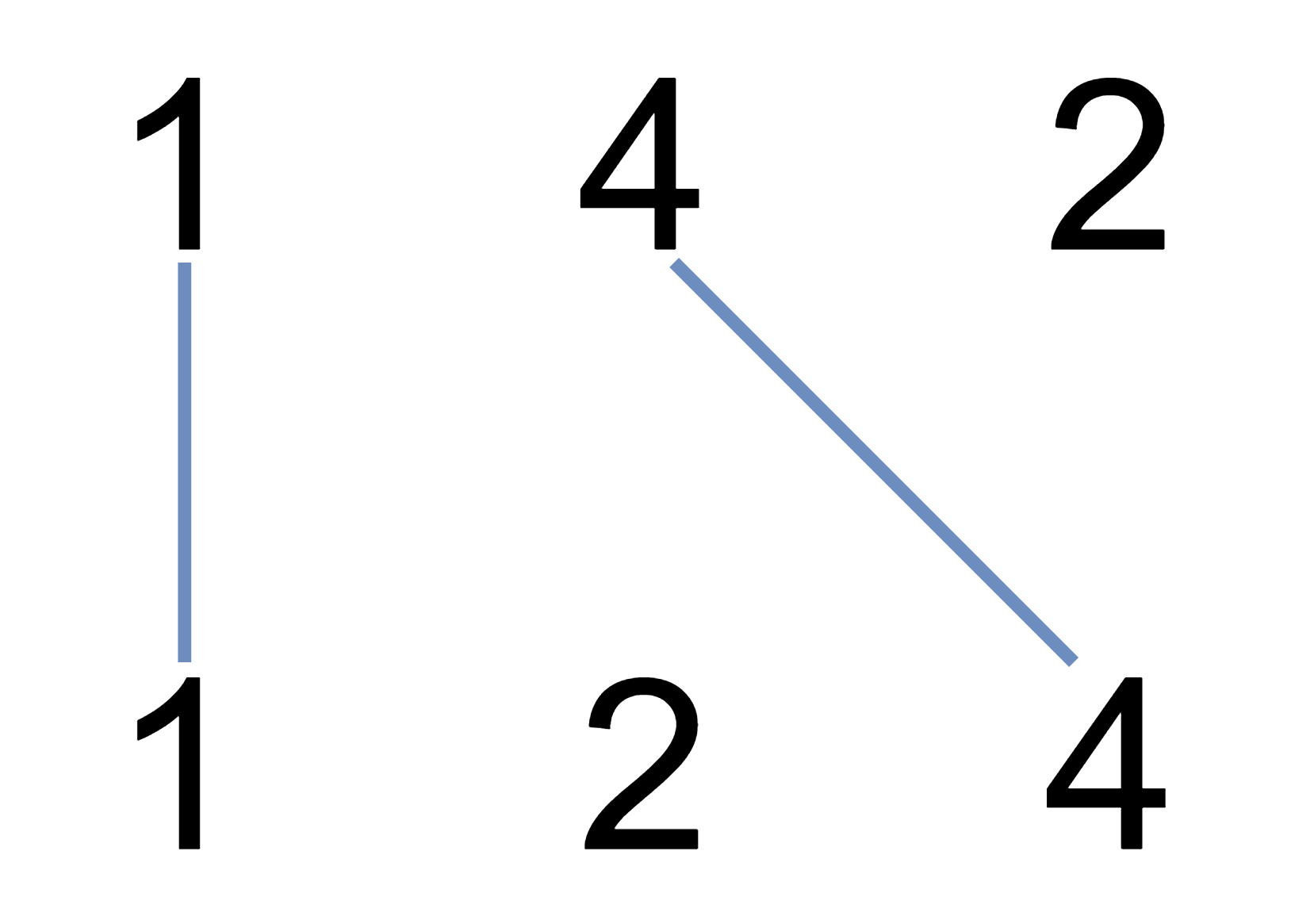
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.

Example 2:

Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3

Example 3:

Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2

Note:

1. 1 <= A.length <= 500
2. 1 <= B.length <= 500
3. 1 <= A[i], B[i] <= 2000

Dynamid programing, my code:
.

Given a binary array, find the maximum length of a contiguous subarray with equal number of 0 and 1.

Example 1:

Input: [0,1]
Output: 2
Explanation: [0, 1] is the longest contiguous subarray with equal number of 0 and 1.

Example 2:

Input: [0,1,0]
Output: 2
Explanation: [0, 1] (or [1, 0]) is a longest contiguous subarray with equal number of 0 and 1.

Note: The length of the given binary array will not exceed 50,000.

This problem i posted.

Given a set of N people (numbered 1, 2, ..., N), we would like to split everyone into two groups of any size.

Each person may dislike some other people, and they should not go into the same group. 

Formally, if dislikes[i] = [a, b], it means it is not allowed to put the people numbered a and b into the same group.

Return true if and only if it is possible to split everyone into two groups in this way.

Example 1:

Input: N = 4, dislikes = [[1,2],[1,3],[2,4]]
Output: true
Explanation: group1 [1,4], group2 [2,3]

Example 2:

Input: N = 3, dislikes = [[1,2],[1,3],[2,3]]
Output: false

Example 3:

Input: N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
Output: false

Constraints:

• 1 <= N <= 2000
• 0 <= dislikes.length <= 10000
• dislikes[i].length == 2
• 1 <= dislikes[i][j] <= N
• dislikes[i][0] < dislikes[i][1]
• There does not exist i != j for which dislikes[i] == dislikes[j].

Graph theory Bipartition, show my code:
.Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1's in their binary representation and return them as an array.

Example 1:

Input: 2
Output: [0,1,1]

Example 2:

Input: 5
Output: [0,1,1,2,1,2]

Follow up:

• It is very easy to come up with a solution with run time O(n*sizeof(integer)). But can you do it in linear time O(n) /possibly in a single pass?
• Space complexity should be O(n).
• Can you do it like a boss? Do it without using any builtin function like __builtin_popcount in c++ or in any other language.

Bitwise operator, my code:
Thank you !